Rezistorul și legile lui Ohm și Kirchhoff

Rezistența electrică
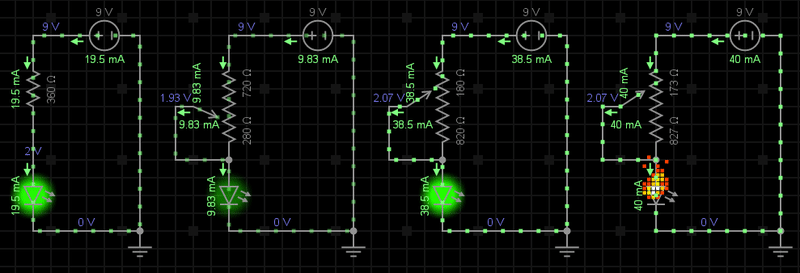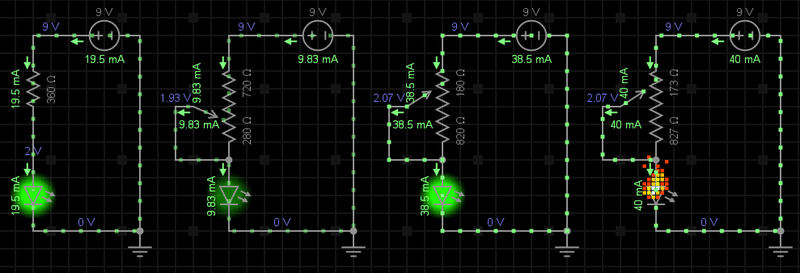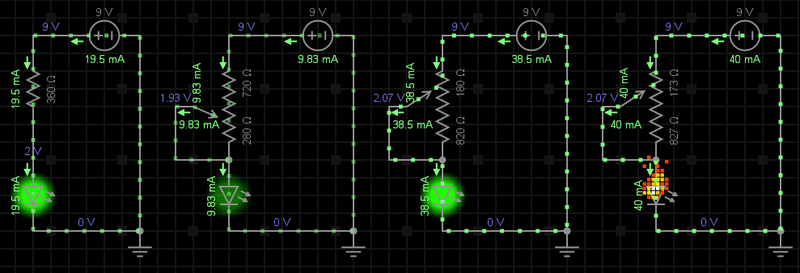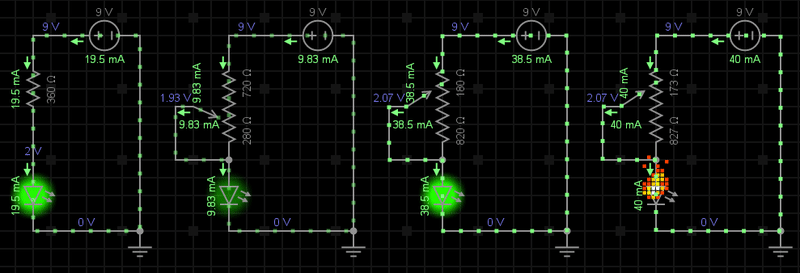
Rezistența electrică îndeplinește două funcții de bază în electronică: limitează curentul și setează nivelul de tensiune într-un circuit. Cea mai simplă aplicație în care se poate demonstra necesitatea unui rezistor o constituie aprinderea unei diode LED (fig. 1). În cazul de față, fără un rezistor care să limiteze curentul prin diodă, aceasta va primi o cantitate excesivă de curent, conducând într-un final la distrugerea (arderea) acesteia.

Pentru o exemplificare și mai concretă, vom înlocui această rezisență de valoare fixă cu una de valoare variabilă (potențiometru). Vei observa acum că odată cu creșterea valorii rezistenței (720 Ω) curentul prin diodă va scădea (9.83 mA), drept pentru care LED-ul va lumina din ce în ce mai încet. Odată cu scăderea valorii rezistorului (180 Ω), dioda va începe să lumineze din ce în ce mai tare și deci curentul pe aceasta să crească (38.5 mA), fiind predispusă în același timp și la ardere. Când valoarea rezistenței scade sub 173 Ω și deci curentul ce străbate dioda LED este mai mare sau egal cu 40 mA, dioda este distrusă.

Legea lui Ohm
Într-un circuit, intensitatea (I) curentului electric este direct proporțională cu tensiunea (U) aplicată și invers proporțională cu rezintența (R) din circuit. Instrumentul pentru măsurarea rezistențelor electrice este ohmetrul. Rezistența se poate măsura și indirect, măsurând tensiunea și intensitatea și făcând apoi raportul dintre mărimile acestora. Pentru a afla puterea disipată de către un rezistor (sub formă de căldură), aplicăm legea puterii care spune că: produsul între tensiunea electrică (U) aplicată la bornele unui consumator şi intensitatea curentului electric (I) ce-l străbate reprezintă puterea electrică (P) a consumatorului respectiv în timpul funcţionării.

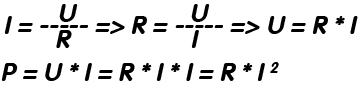
Foarte rare sunt circuitele în care se folosesc doar o singură rezistență. De obicei acestea se găsesc conectate într-o varietate de moduri, însă cele două metode fundamentale de conectare sunt: serie și paralel.

Legarea rezistențelor în paralel
Când două sau mai multe rezistențe sunt conectate în paralel, tensiunea la bornele fiecărui rezistor este aceeași, iar curentul ce-l străbate variază în funcție de valoarea acestuia. De asemenea valoarea rezistenței totale a întregului ansamblu de rezistoare va fi mai mică decât cea mai mică rezistență conectată în combinația utilizată. Formula de calcul a rezistenței totale în cazul legării paralel este dată de expresia:

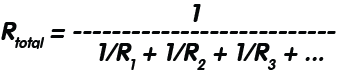
Exemplu: Presupunem 2 rezistențe conectate în paralel, R1 = 1kΩ și R2 = 3kΩ, alimentate de la o sursă de tensiune de curent continuu de 9V, deci U = 9V. Aflați valoarea rezistenței totale Rt cât și valoarea tensiunii și curenților ce străbat aceste rezistențe (vezi fig. 2).

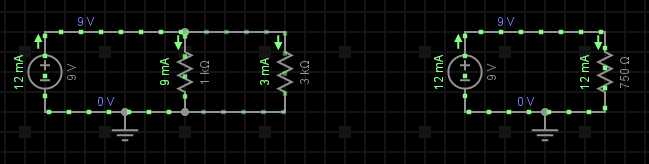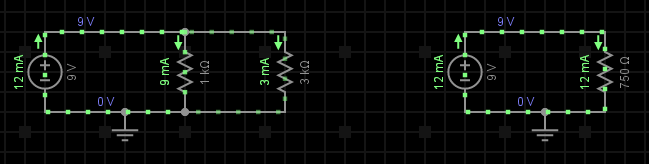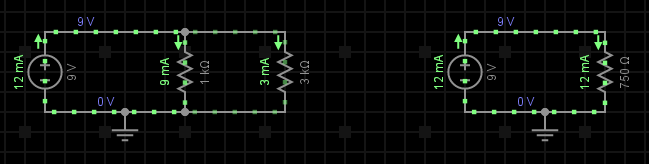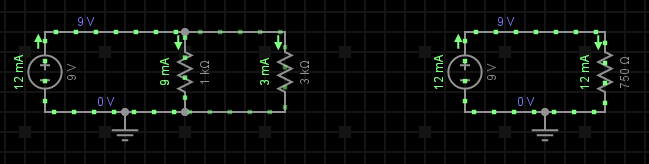
Pasul 1: Cunoscând valoarea căderii de tensiune U pe ambele rezistențe (care e aceeași deoarece avem legare tip paralel), vom determina pe rând valoarea celor doi curenți I1 și I2, curenți ce străbat cele 2 rezistențe din circuit:

Pasul 2: Calculăm valoarea rezistenței totale a circuitului, Re:

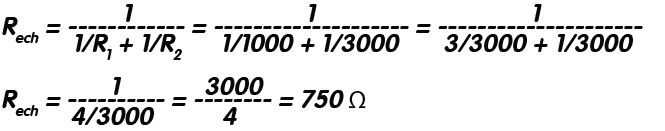
Pasul 3: După aflarea valorii rezistenței echivalente, calculăm valoarea curentului total ce străbate circuitul:

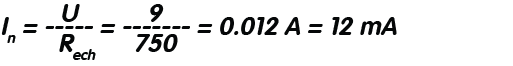
După cum se poate observa, în nodul de rețea ilustrat cu ajutorul cercului roșu, întră curentul In de 12mA și ies doi curenți: I1 de 9mA și I2 de 3mA (calculați anterior). La o examinare mai atentă se poate observa că suma curenților ce ies din acel nod este egală cu suma curenților care întră în el, fiind astfel enunțată prima lege a lui Kirchhoff:

Legarea rezistoarelor în serie
Atunci când 2 sau mai multe rezistoare sunt legate în serie (fig. 3), rezistența totală este calculată ca sumă a tuturor rezistențelor independente legate între ele. De asemenea, curentul ce strabate toate aceste rezistențe conectate în serie este același, în timp ce tensiunea la bornele fiecărui rezistor este diferită, în funcție de fiecare valoare a sa în parte (exprimată în Ohm).
Formula generală de calcul a legării serie este:

Exemplu: Presupunem 2 rezistențe conectate în serie, R1 = 1kΩ și R2 = 2kΩ, alimentate de la o sursă de tensiune de curent continuu de 9V, deci U = 9V. Aflați valoarea rezistenței totale Rt cât și valoarea tensiunii și curenților ce străbat aceste rezistențe (vezi fig. 3).

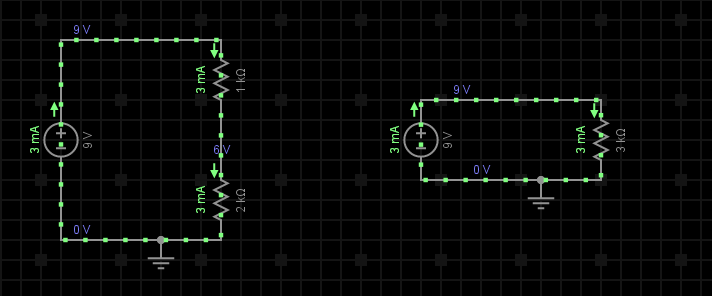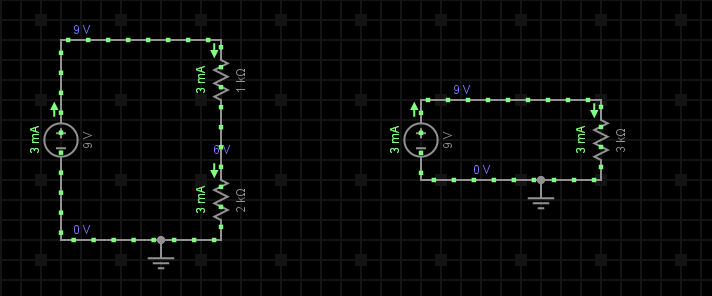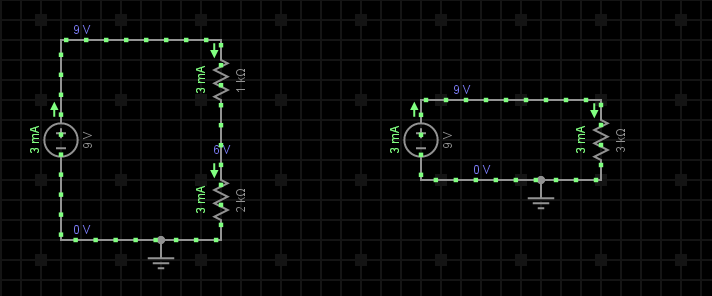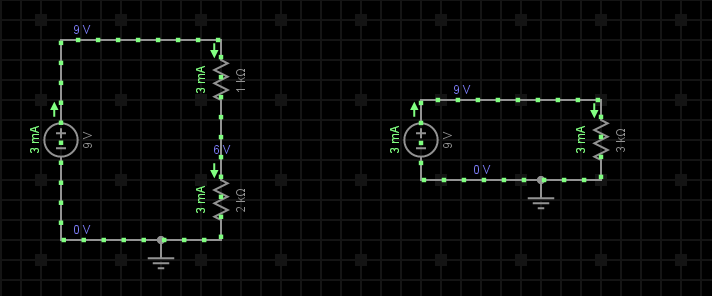
Pasul 1: Cunoscând valoarea tensiunii de alimentarea a circuitului, U, vom determina mai întâi valoarea rezistenței echivalente a întregului circuit pentru a putea calcula mai apoi valoarea curentului ce strabate cele 2 rezistoare:

Pasul 2: Cunoscând acum valoarea rezisteței echivalente a circuitului (fig. 3b), precum și tensiunea de alimentarea a acestuia, aplicând legea lui Ohm vom obține valoarea curentului ce strabate întreg circuitul:

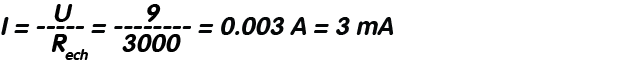
Pasul 3: Având toate datele necesare (tensiune, respectiv curent), vom calcula caderile de tensiune de la bornele celor 2 rezistoare:

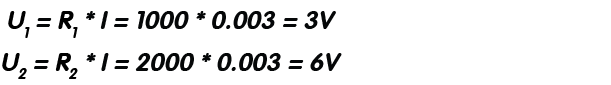
Legile lui Kirchhoff
Mai mult ca sigur, odată cu stăpânirea cunoștiințelor de bază, vei ajunge să parcurgi și să citești scheme electrice din ce în ce mai complexe, scheme în care legea lui Ohm sau cunoștiințele asupra legării serie și paralel a rezistoarelor nu va fi îndeajuns încât să înțelegi întregul principiu de funcționare a schemei respective (ca de exemplu o schemă electrică în care se găsesc 2 sau mai multe surse de tensiune). Legile lui Kirchhoff ne oferă o metodă generală de analiză a tuturor circuitelor. Aceste legi funcționează pentru componente precum: rezistențe, condensatoare, bobine, cât și pentru: diode, tranzistoare, etc.

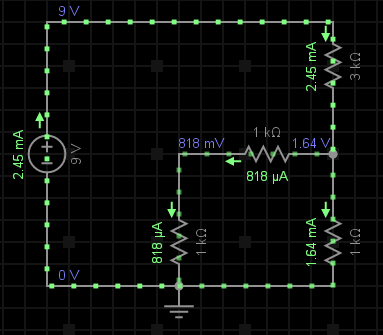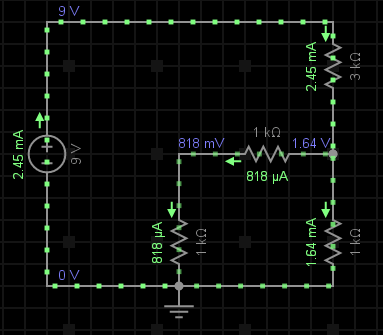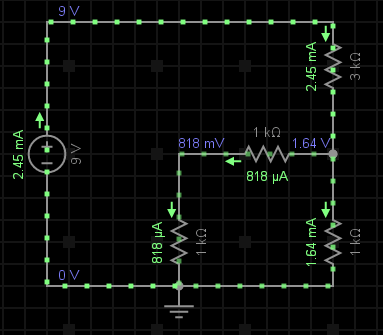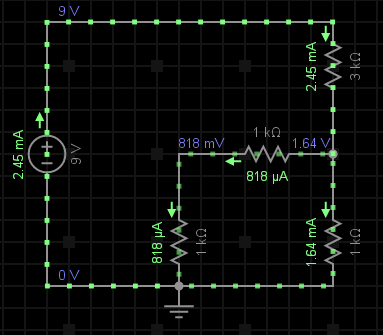
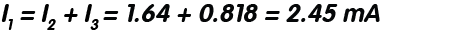
Legea ochiurilor de rețea (A doua lege a lui Kirchhoff)
De-a lungul unui ochi de rețea, suma algebrică a tensiunilor electromotoare ale surselor este egală cu suma algebrică a produselor dintre intensitatea curenților și rezistența totală de pe fiecare latură.

Pasul 2: Identificăm laturile, iar mai apoi pe fiecare dintre ele notăm sensul și numele curenților ce le străbat (de regulă, acestea vor fi necunoscutele). Se poate observa pe figura noastră că dispunem de 6 astfel de laturi, fiind deja evidențiată direcția și notația celor 6 curenți.

Pasul 3: Identificăm fiecare ochi de rețea, adică linia poligonală închisă formată din 3 sau mai multe laturi de rețea.

Pasul 4: Aplicăm prima lege a lui Kirchhoff, obținând următoarele ecuații:
Nodul a:
Nodul b:
Nodul c:

Pasul 5: Aplicăm a doua lege a lui Kirchhoff pe toate ochiurile de rețea a circuitului nostru. După cum se poate observa în schema electrică a circuitului, dispunem de 3 astfel de ochiuri:
Ochiul 1: Avem o singură sursă de tensiune, U0 și 3 laturi de unde rezultă că:

Ochiul 2: Se observă că nu avem nici o sursă de tensiune ci doar 3 laturi:

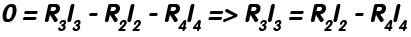
Ochiul 3: 3 laturi și aici și nici o sursă de tensiune:

Pasul 5: Adunăm toate cele 6 ecuații de mai sus sub forma unui sistem de funcții după care, folosind metoda lui Cramer de rezolvare a sistemelor liniare, vom obține următorul determinant:

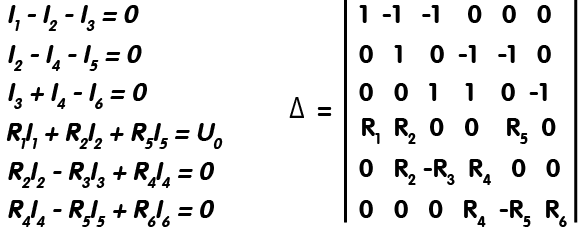
Acum, pentru a găsi de exemplu valoarea curentului și căderea de tensiunea la bornele rezistorului R5, găsim mai întâi ΔI5, iar apoi aplicăm formula:, pentru a găsi valoarea curentului. Ulterior, știind curentul și valoarea rezistenței, aplicând legea lui Ohm, vom afla și tensiunea la bornele ei.

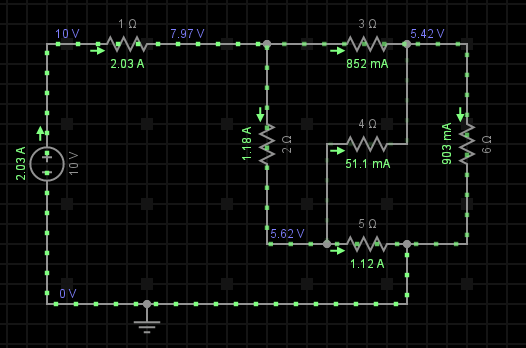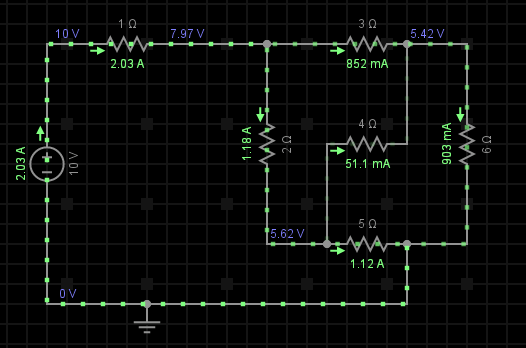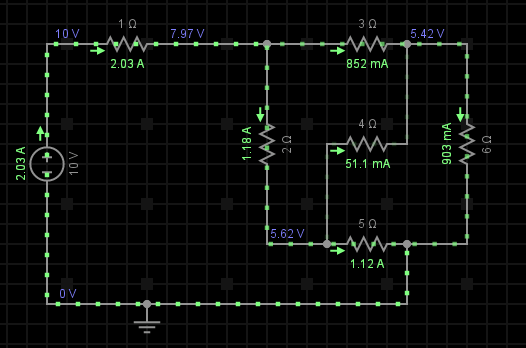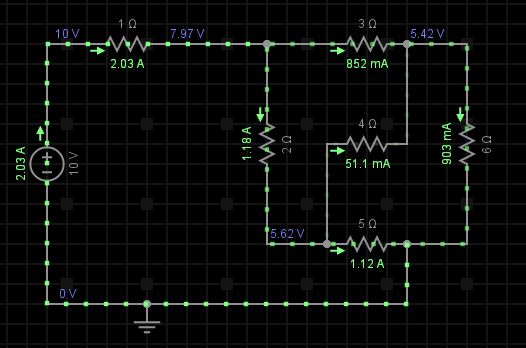
Cam atât pentru azi, în zilele ce urmează vom vorbi puțin dispozitivele electrice utilizate la înmagazinarea de energie în câmp magnetic (bobine), respectiv câmp electric (condensatoare).